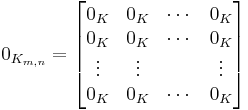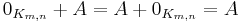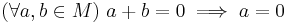List of zero terms

The number 0 is an important concept in mathematics.

1 Zero module
2 Zero ideal
3 Zero matrix
4 Zero tensor
5 Zero divisor
6 Zerosumfree monoid
7 Zero set
8 Zero order
9 See also

Zero module

In mathematics, the zero module is the module consisting of only the additive identity for the module's addition function. In the integers, this identity is zero, which gives the name zero module. That the zero module is in fact a module is simple to show; it is closed under addition and multiplication trivially.

Zero ideal

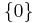In mathematics, the zero ideal in a ring $R$ is the ideal $\{ 0 \}$ consisting of only the additive identity (or zero element). It is immediate to show that this is an ideal.

Zero matrix

In mathematics, particularly linear algebra, a zero matrix is a matrix with all its entries being zero. Some examples of zero matrices are

$0_{1,1} = \begin{bmatrix} 0 \end{bmatrix} ,\ 0_{2,2} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} ,\ 0_{2,3} = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} ,\$

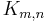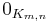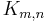The set of m×n matrices with entries in a ring K forms a module $K_{m,n} \,$ . The zero matrix $0_{K_{m,n}} \,$ in $K_{m,n} \,$ is the matrix with all entries equal to 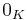$0_K \,$ , where 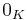$0_K \,$ is the additive identity in K.

$0_{K_{m,n}} = \begin{bmatrix} 0_K & 0_K & \cdots & 0_K \\ 0_K & 0_K & \cdots & 0_K \\ \vdots & \vdots & & \vdots \\ 0_K & 0_K & \cdots & 0_K \end{bmatrix}$

The zero matrix is the additive identity in 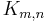$K_{m,n} \,$ . That is, for all 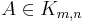$A \in K_{m,n} \,$ it satisfies

$0_{K_{m,n}}%2BA = A %2B 0_{K_{m,n}} = A$

There is exactly one zero matrix of any given size m×n having entries in a given ring, so when the context is clear one often refers to the zero matrix. In general the zero element of a ring is unique and typically denoted as 0 without any subscript indicating the parent ring. Hence the examples above represent zero matrices over any ring.

The zero matrix represents the linear transformation sending all vectors to the zero vector.

Zero tensor

In mathematics, the zero tensor is any tensor, of any rank, all of whose entries are zero. The zero tensor of rank 1 is sometimes known as the null vector.

Taking a tensor product of any tensor with any zero tensor results in another zero tensor. Adding the zero tensor is equivalent to the identity operation.

Zero divisor

A zero divisor in a ring R is an element a ∈ R such that ab = 0 for some non-zero b ∈ R.

Zerosumfree monoid

In abstract algebra, an additive monoid 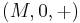$(M, 0, %2B)$ is said to be zerosumfree if nonzero elements do not sum to zero. Formally:

$(\forall a,b\in M)\ a %2B b = 0 \implies a = 0 \!$

This means that the only way zero can be expressed as a sum is as 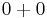$0 %2B 0$ .

Zero set

In mathematics, the zero set of a real-valued function f is the inverse image 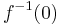$f^{-1}(0)$ .

Zero order

A zero order process is one in which past behavior does not affect the future outcome. For example, in marketing, the zero order hypothesis holds that the brands you will purchase next will not depend on the brands you have purchased before. That means you have a fixed probability of purchase. Contrast it to the first order process when the outcome at time t-1 changes the outcome at time t.